Neural Networks

Neurons assemble!

In my last post about back propagation, we looked at a single neuron and did forward and backward propagation. We learnt a little about how to nudge things in the right direction with gradient descent.

In terms of code, we had a neuron that looked a little like this:

// Given some input, calculate the output using the internal weights + bias
public double FeedForward(double x1, double x2);

// Given some output, adjust the internal weights + bias to minimize error.
public void Backpropagate(double x1, double x2, double error, double learningRate);

In this post, we’ll see why a single neuron isn’t enough by trying to solve a classic problem (XOR). Then we’ll assemble neurons into layers, and layers into networks. Then we’ll try and solve a real problem using the MNIST data set.

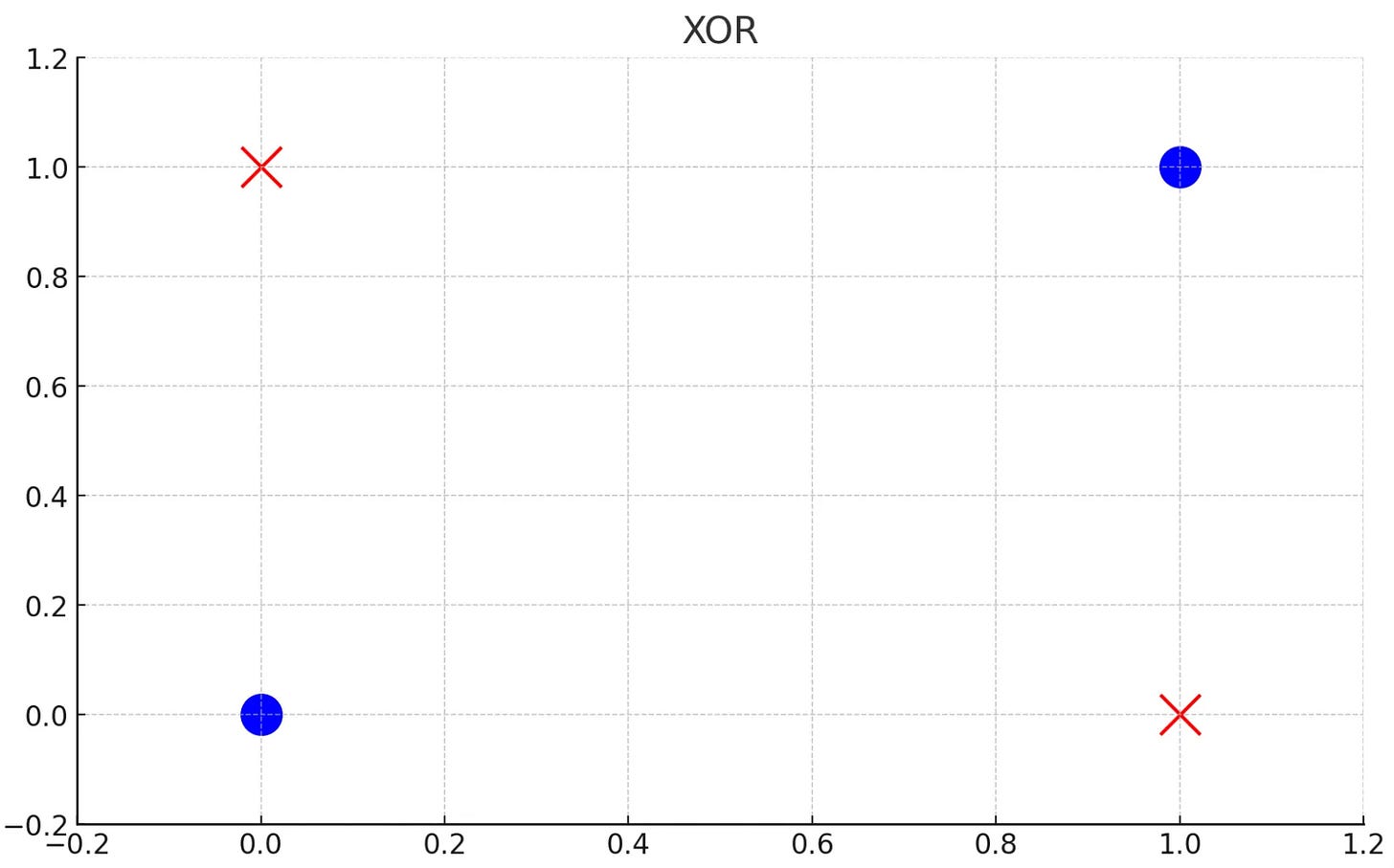
OR was easy; let’s try XOR!

We trained our single neuron to solve the OR problem, and it worked! Let’s try XOR! XOR (denoted by ⊕) returns one if exactly one of its arguments is one. For example

1 ⊕ 1 = 0
1 ⊕ 0 = 1
0 ⊕ 1 = 1
0 ⊕ 0 = 0

So, with our single neuron, our challenge is to find some weights and a bias to give the right answer.

If you’ve got some time, try it out using the back-propagation code - you’ll find it’ll never give you the right answer. Why is that?

This happens because XOR is not linearly separable. To put that simply, you can’t draw a straight line that divides the 1s and 0s!

A single neuron can’t solve a non-linear problem. Can we prove this?

Well, for these simple examples neural networks are finding the solution to the formula below.

\(\begin{align*} y&=\sigma(w_1x_1+w_2x_2) \\ \sigma(z)&=\frac{1}{(1+e^{-z})} \end{align*} \)

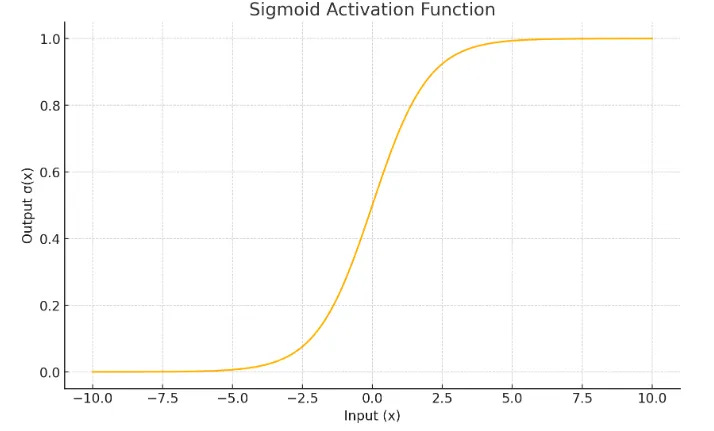
This looks hard to solve, but since we’re only thinking about zeros and ones, we can be a bit more intuitive. In order for the sigmoid activation function to produce 0, its value needs to be a large negative number. Similarly, for it to produce one, the value needs to be a huge positive number.

The Sigmoid activation function

Let’s look at each of the four cases and look at what it implies about the weights and bias.

\(\begin{aligned}(0,0)\to0: &\quad b < 0, \\[6pt](1,0)\to1: &\quad w_1 + b > 0, \\[6pt](0,1)\to1: &\quad w_2 + b > 0, \\[6pt]\text{Add the last two:}&\quad w_1 + w_2 + 2b > 0, \\[6pt]\text{Subtract }b\text{ from both sides:}&\quad w_1 + w_2 + b > -\,b, \\[6pt]\text{But since }b<0\Rightarrow -b>0:&\quad w_1 + w_2 + b > 0, \\[6pt](1,1)\to0: &\quad w_1 + w_2 + b < 0, \\[6pt]\therefore &\quad\text{Contradiction i.e. we're screwed}\end{aligned}\)

Let’s look at how we solve this by connecting multiple neurons together.

Combining Neurons into Layers

Our problem is that we can’t do a straight line separating the XOR. How can we fix that? The answer is to just cheat - instead transform the data into a new space where we can draw a line between them. That sounds like a quote from the Matrix, but it’s not!

To get the general gist, grab a square bit of paper and colour opposite corners in. Now just bend the bit of paper so you can draw a straight line between them. For example, in the below if I pull the blue corner together (higher than red!) then there’s a line separating the classes now.

A tool for visualizing linear space transformations

That’s what the hidden layers help us do - they represent that intermediate space and thanks to the non-linear activation function (sigmoid) they are a funkier shape (a much funkier shape in many more dimensions).

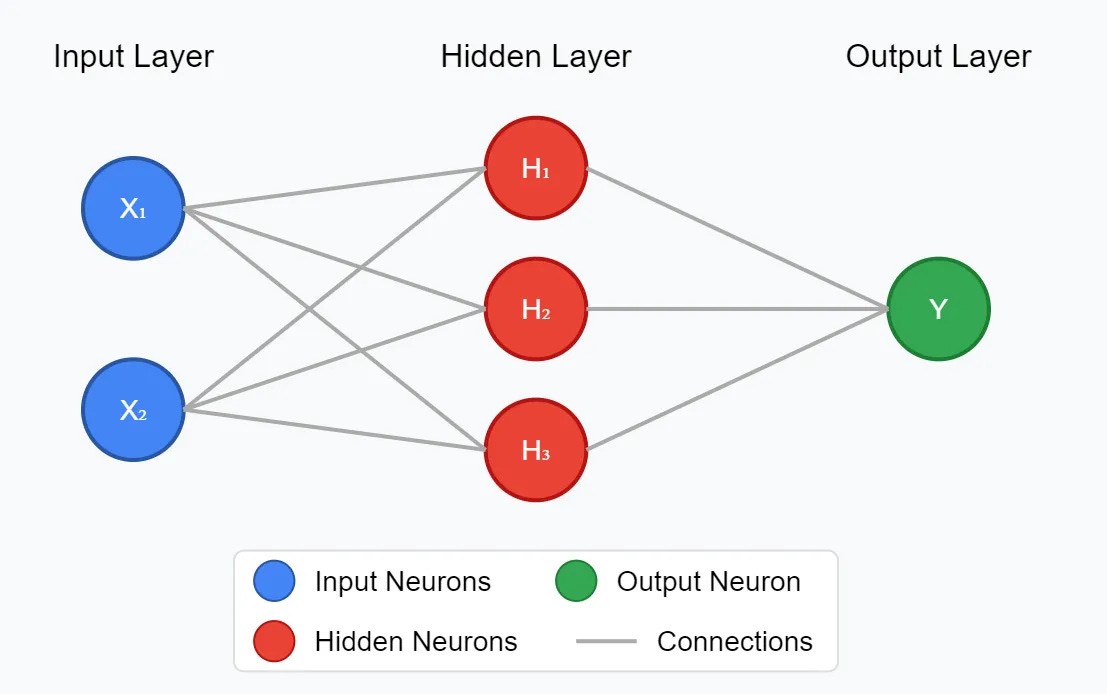
For our XOR problem, we’ve got 2 inputs and 1 output. Let’s shove a layer in the middle.

Remember from last time, our neuron did the following two jobs. Given some inputs, multiply it by the weights and give an output (FeedForward ), and given an error for given inputs nudge the weights in the right direction and return the errors (back propagation).

Layers do exactly the same thing, they take some inputs, multiply it by all the weights and give an output, and do the reverse. This self-similarity extends to the network as a whole - they all just go forward and update backwards. If you can understand a single neuron, then you’ve basically groked neural networks.

Let’s start with feed forward. Here’s some fragments from the neuron, then the layer and finally the network as a whole.

// A single neuron is just the activation function applied to weights * inputs + bias
Sigmoid(Vector.DotProduct(_weights, inputs) + _bias);

// A layer gives us one output for each neuron
new Vector(_neurons.Select(n => n.FeedForward(inputs)).ToArray())

// And finally a neural network feeds the output of one layer to the next until done
// Aggregate is the same as fold, you can think of this as
// layer.FeedForward(inputLayer.FeedForward(inputs)) for two layers
_layers.Aggregate(inputs, (currentOutputs, layer) => layer.FeedForward(currentOutputs));

The back propagation part applies similar logic, except backwards. Each neuron calculates how wrong it was and updates its weights. A layer collects these errors and passes them backward, layer by layer.

// The neuron uses the Sigmoid derivative to adjust 
  double sigmoidDeriv = SigmoidDerivative(_lastOutput);
  double delta = error * sigmoidDeriv;            
  Vector errors = delta * _weights;
  _weights += learningRate * delta * inputs;        
  _bias += learningRate * delta;  
  return errors;
  
// A layer gets some inputs, the errors for this layer.
// For each neuron it calculates the error and finally, returns the errors
// accumulated to the previous layer to propagate backwards.
_neurons.Select((neuron, i) => neuron.Backpropagate(inputs, errors[i], learningRate))
  .Aggregate(
    new Vector(inputs.Length), // Start with a zero vector of the right size
    (accumulatedErrors, neuronErrors) => accumulatedErrors + neuronErrors
  );
  
// Finally, for the network, we go through the layers backwards and 
// call back propagate (activations 
Enumerable.Range(0, _layers.Count)
  .Reverse()
  .Aggregate(
    outputErrors,
    (currentErrors, i) => 
      _layers[i].Backpropagate(_activations[i], currentErrors, learningRate)
);   

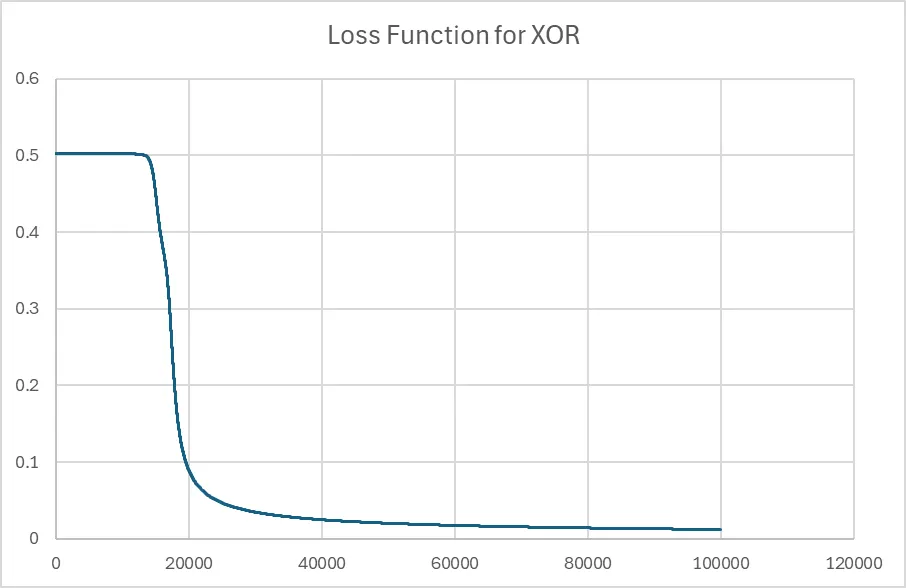
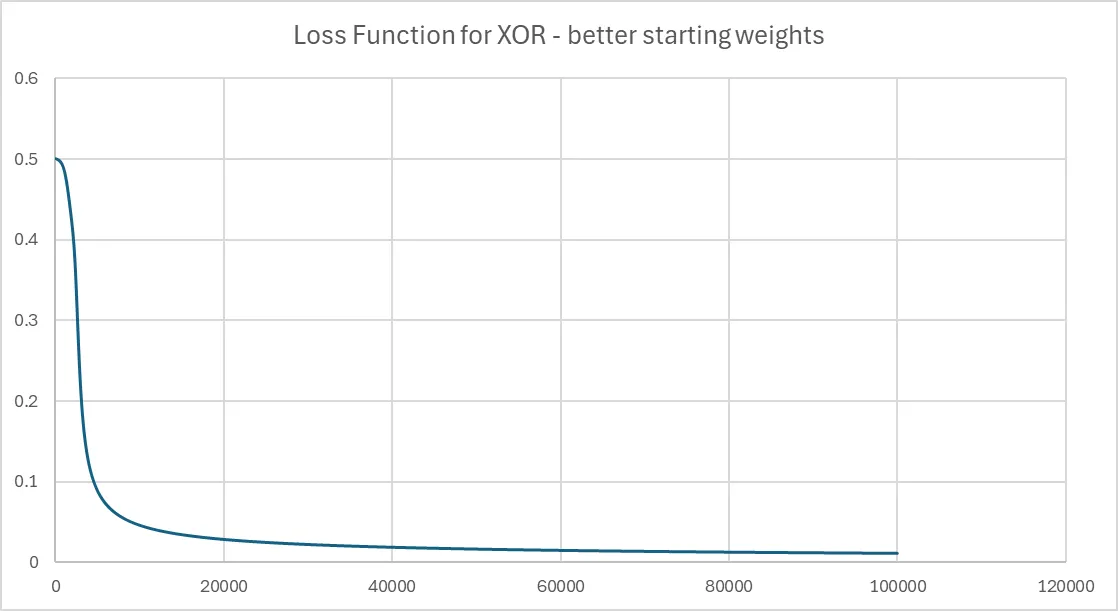
To train the network, we just loop repeat feed forward, calculate the errors and back propagate until we converge. And if we do that and print out the loss function we get something like:

Why the big flat bit at the start? That’s because I picked the initial weights poorly (random numbers between -0.1 and 0.1). We started on a really flat area of the loss function, and it took a long time to navigate across to a valley.

If instead we initialize the weights using a specific technique (Xavier initialization), then results are much improved. Xavier initialization means the weights aren’t too small (which slows down learning) or too large (which causes unstable training).

  // Xavier initialization
  _weights = new Vector(inputSize);
  double sqrtVariance = Math.Sqrt(1.0 / inputSize);
  for (int i=0; i < _weights.Length; i++)
      _weights[i] = _random.NextGaussian(0, sqrtVariance);

  _bias = _random.NextGaussian(0, sqrtVariance);

And if we print out the loss function now, then it looks more typical.

I’ve put all the code for this at Neurons Assemble. I’ve tried to make the code easy to understand and avoid any third-party libraries (rather than highly performing - if you haven’t guessed this is a disclaimer!). If you want it to go brrrr then I imagine replacing the Vector implementation with something from Math.Numerics will be a huge boost (but at a minimum run it in Release mode or you’ll be waiting forever).

Can we do something more complicated?

Let’s see how we do on the MNIST standard set. This is a recognition challenge (in fact it’s one of the most famous ones). Given a hand-written digit, can you correctly get the number?

Sample MNIST images from Wikipedia

Let’s create a neural network to solve this problem.

Each image is 28x28. We’ll just turn that into a single vector of size 784 (28 x 28!). As output we want to know what digit it is. There are ten possibilities (0-9), so we use a vector of size 10.

So, that means we need 784 to start, and 10 at the end. What about the bit in the middle? How many hidden layers should we have? How many neurons in each layer? I’ve no idea! So I picked fifty, primarily because that number meant it took exactly one dog walk to train the model.

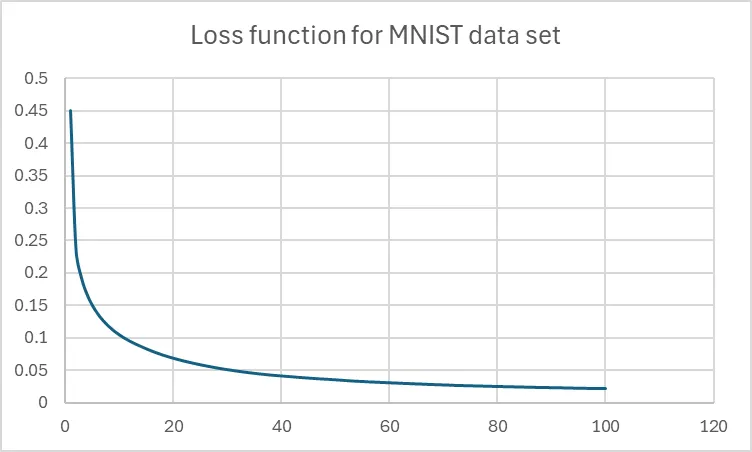
How does our bare-bones system do? Pretty damn well (at least in the training phase)

One dog-walk run of training

I stopped it after hundred iterations because I’m not very patient, but it was still converging and the value was average absolute loss was 0.02. This means that on the training set, we’ve managed to almost exactly fit the data (i.e. on the training set at least, the neural network will get almost everything exactly right). Note that this doesn’t mean it’s any good (we might have over-fitted to the training data and find that it doesn’t generalize).

Conclusion

Hopefully, this post has shown that once you understand a single neuron you’ve got all the building blocks you need to create a neural network. These same general principles (albeit with some fancy embellishments) power all neural networks that you see, including ChatGPT and friends.

It’s worth the effort to understand neural networks. They sound mysterious and complicated, but really it’s some multiplication and differentiation. That’s it!

Happy hacking!